| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- bfs문제
- BFS
- sort
- 삼성역테
- MCU 딥러닝
- 포스코 ai 교육
- 코테 문제
- 삼성코딩테스트
- 영상처리
- 삼성코테
- 초소형머신러닝
- TensorFlow Lite
- 알고리즘
- tinyml
- 코딩테스트
- 컴퓨팅사고
- dfs문제
- 딥러닝
- tflite
- 임베디드 딥러닝
- 자료구조
- DP
- 포스코 AI교육
- DP문제
- 포스코 교육
- 코테
- 삼성역량테스트
- 다이나믹프로그래밍
- 그리디
- dfs
- Today
- Total
코딩뚠뚠
[머신러닝 공부] 6. 비용 함수 1 본문
머신러닝 입문자들의 필수코스라고 할 수 있는 앤드류 응 님의 강의를 번역해놓은 아래 브런치를 참고하여 공부하고 핵심내용만 정리해보고자 한다.
원문 출처 : brunch.co.kr/@linecard/443
앤드류 응의 머신러닝 강의 (2-2) : 비용 함수
온라인 강의 플랫폼 코세라의 창립자인 앤드류 응 (Andrew Ng) 교수는 인공지능 업계의 거장입니다. 그가 스탠퍼드 대학에서 머신 러닝 입문자에게 한 강의를 그대로 코세라 온라인 강의 (Coursera.org
brunch.co.kr
비용함수 : Cost Function
비용함수는 데이터에 가장 잘 맞는 최적의 직선을 찾는다.

위의 사진은 앞강의에서 예측(predict)을 위해 사용했던 선형함수 h(x)이다. (h=Hypothesis=가설)
가설에서 θ 로 표현되는 것은 파라미터이다.
위 사진에서 2개의 파라미터 θ0 θ1의 값을 고르는 방법을 이 포스팅에서 설명할 것이다.
θ0과 θ1의 값에 따라서 선형함수인 h(x)의 기울기는 달라질 것이다.
θ0과 θ1 고르기
-> 선형회귀에서 학습 데이터 셋을 그래프에 도식화 해본다.
-> θ0과 θ1을 이용해 데이터 셋을 도식화 한 것에 근접한 기울기로 직선을 그린다.
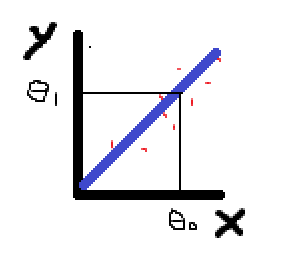
-> 일치도를 확인한다. (즉 θ0과 θ1을 선택한 후 x의 값에 따른 예측값 hθ(x)와 y가 얼마나 가까운지를 확인하는 것.)
공식화
선형회기 문제는 파라미터 θ0과 θ1을 최소화하는 문제를 해결하는 의미이다.
-> hθ(x)와 y의 차이를 최소화 한다.
( 가설(h) 의 결과값과 실제값(y)의 차이의 제곱을 최소화 한다. )

-> 실제 학습데이터 셋의 i=1부터 m까지의 제곱의 합계를 구한다.
( 위의 작업을 반복하여 sum 하는것 )
( (x^(i),y^(i))는 i번째 학습데이터를 뜻한다.)

-> 합산에 대한 평균을 계산하기 위해 학습 데이터셋의 개수 m 으로 나눠주고 미분을 했을 때 수식을 단순화하기 위해 2로 나눠준다.
( x^(i)는 i번째 데이터의 값, hθ(x^(i))는 i번째 x 데이터로 예측한 값이다. )
( 현재 과정은 평균오차의 제곱의 절반을 최소화하는 파라미터의 값θ을 구하는 과정이다. )
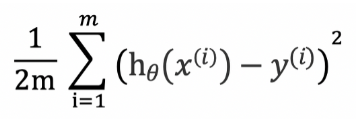
-> hθ(x^(i)-y^(i))를 최소화 한다는 것은 파라미터 θ0 θ1 을 최소화 하는것과 같다
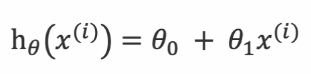
여기서 다룬 θ0 θ1을 최소화 하는 함수를..
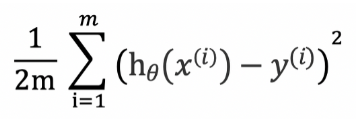
제곱오차함수 즉 비용함수 라고 부른다. 이는 대부분의 회기(regression)문제에서 잘 동작한다.
참고자료 : 회기 regression 와 분류 classification 차이
dbstndi6316.tistory.com/164?category=957031
[머신러닝 공부] 3. 지도학습
머신러닝 입문자들의 필수코스라고 할 수 있는 앤드류 응 님의 강의를 번역해놓은 아래 브런치를 참고하여 공부하고 핵심내용만 정리해보고자 한다. 원문 출처 : brunch.co.kr/@linecard/439 앤드류 응
dbstndi6316.tistory.com
'공부 > ML&DL' 카테고리의 다른 글
| [머신러닝 공부] 8. 비용 함수 3 (0) | 2021.01.19 |
|---|---|
| [머신러닝 공부] 7. 비용 함수 2 (0) | 2021.01.12 |
| [머신러닝 공부] 5. 가설의 표현 (0) | 2021.01.05 |
| [머신러닝 공부] 4. 비지도학습 (0) | 2021.01.05 |
| [머신러닝 공부] 3. 지도학습 (0) | 2021.01.05 |


